新課標的一個重要課程目標是利用數學知識解決生活中的實際問題，是學生學習知識、形成技能和發展為能力的結果，也是學生具備了建模思想的重要標志。

　　構建數學模型解決實際問題基本步驟如下：

　　1、閱讀、審題：

　　要做到簡縮問題，刪掉次要語句，深入理解關鍵字句；為便于數據處理，最好運用表格（或圖形）處理數據，便于尋找數量關系。

　　2、建模、建立數學關系式：

　　將問題簡單化、符號化，盡量借鑒標準形式，建立數學關系式。

　　3、運用數學知識

　　4、解釋并回答實際問題

　　為了更加形象表示，我們可以參考下面的圖標：

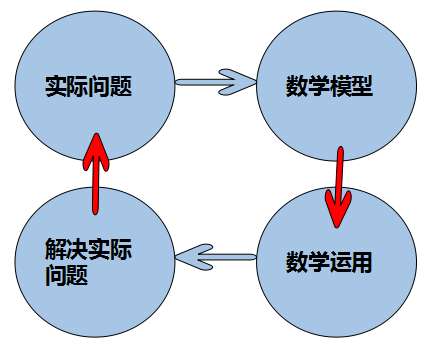
　　那么一起來看看數學和生活實際問題在中考中是怎么體現：

　　一、方程模型的應用

　　基本步驟：設元、列方程、解方程。解應用題的關鍵是：尋找題目中的等量關系，尤其是從語言中挖掘等量關系。找等量關系實際上就是從實際問題到建立數學模型的一個過渡階段。

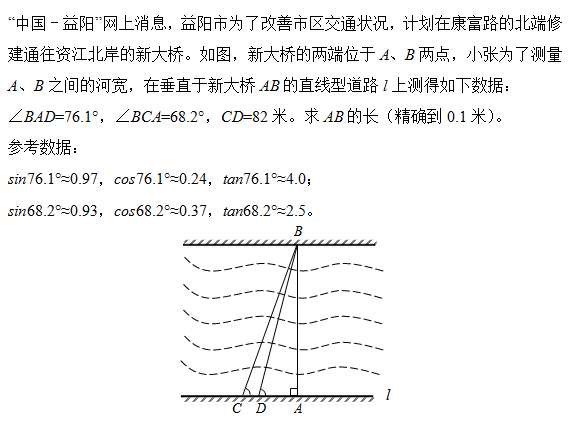
　　下面以2014年益陽的第18題為例：

　　二、方程不等式模型的綜合應用

　　在解決方案型問題時，可由方程模型建立多個未知數之間的關系，最終通過代換消元，得到不等式中的整數解，進而得出幾種方案。

　　下面以2014年貴州黔東南州第23題為例：

　　某超市計劃購進一批甲、乙兩種玩具，已知5件甲種玩具的進價與3件乙種玩具的進價的和為231元，2件甲種玩具的進價與3件乙種玩具的進價的和為141元。

　　（1）求每件甲種、乙種玩具的進價分別是多少元？

　　（2）如果購進甲種玩具有優惠，優惠方法是：購進甲種玩具超過20件，超出部分可以享受7折優惠，若購進x（x＞0）件甲種玩具需要花費y元，請你求出y與x的函數關系式；

　　（3）在（2）的條件下，超市決定在甲、乙兩種玩具中選購其中一種，且數量超過20件，請你幫助超市判斷購進哪種玩具省錢。

　　三、函數模型在最值問題中的應用

　　在最值問題中，如果題中沒有設出自變量，最后讓求最值時，可分析題中哪個量引起另一個的變化，可設這兩個量分別為自變量和函數，建立函數關系式，注意自變量的范圍，如果是一次函數的最值問題，一定要求自變量的取值范圍，結合一次函數的增減性求最值；如果是二次函數的最值問題，利用配方法后，一定要看頂點橫坐標是否在自變量的范圍內，若不在，結合圖像求解。

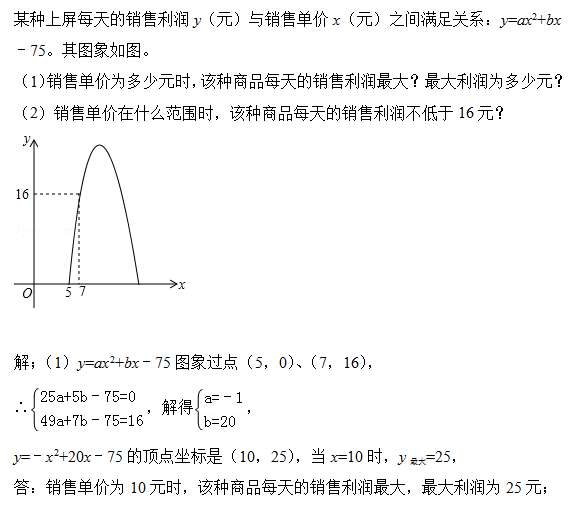
　　下面以2014年江蘇徐州的第26題為例：

　　四、幾何模型的應用

　　構建幾何模型就是把實際問題中本質的東西抽象為幾何圖形（線段、直角三角形，等腰三角形、平行四邊形、梯形等），利用幾何圖形的性質解決實際問題。

　　下面以2014年浙江寧波的第26題為例：